1、概述
1、定义
在计算机科学中,数组是由一组元素(值或变量)组成的数据结构,每个元素有至少一个索引或键来标识
In computer science, an array is a data structure consisting of a collection of elements (values or variables), each identified by at least one array index or key
2、数组的特点:
因为数组内的元素是连续存储的,所以数组中元素的地址,可以通过其索引计算出来,例如:
int[] array = {1,2,3,4,5}
知道了数组的数据起始地址 BaseAddress,就可以由公式 $BaseAddress + i * size$ 计算出索引 i 元素的地址
- i 即索引,在 Java、C 等语言都是从 0 开始
- size 是每个元素占用字节,例如 int 占 4,double 占 8
小测试
byte[] array = {1,2,3,4,5}
已知 array 的数据的起始地址是 0x7138f94c8,那么元素 3 的地址是什么?
答:0x7138f94c8 + 2 * 1 = 0x7138f94ca
3、空间占用
Java 中数组结构为
- 8 字节 markword
- 4 字节 class 指针(压缩 class 指针的情况)
- 4 字节 数组大小(决定了数组最大容量是 2^32^)
- 数组元素 + 对齐字节(Java 中所有对象大小都是 8 字节的整数倍,不足的要用对齐字节补足)
- 这和 JDK 版本有关,64 位 JDK 按 8 字节对齐
例如:
int[] array = {1, 2, 3, 4, 5};
的大小为 40 个字节,组成如下
8 + 4 + 4 + 5 * 4 + 4(补齐)
4、随机访问性能
即根据索引查找元素,时间复杂度是 $O(1)$
2、动态数组
Java 自带的数组无法插入和删除元素,并且大小在创建数组时就已固定,之后无法改变,这种数组称之为静态数组。
与之对应的,如果一个数组能插入或删除元素,并且大小能根据实际需要发生变化,这种数组称之为动态数组。
Java 中其实有实现好的动态数组,就是 ArrayList。但我们要自己实现一个动态数组
Java 版本
public class DynamicArray implements Iterable<Integer> {
private int size = 0; // 逻辑大小
private int capacity = 8; // 容量
// private int[] array = new int[capacity];
private int[] array = {}; // 懒惰初始化
/**
* 向最后位置 [size] 添加元素
* @param element 待添加元素
*/
public void addLast(int element) {
// array[size] = element;
// size++;
add(size, element);
}
/**
* 向 [0 ... size] 位置添加元素
* @param index 索引位置
* @param element 待添加元素
*/
public void add(int index, int element) {
checkAndGrow();
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException();
}
/*if (index >= 0 && index < size) {
System.arraycopy(array, index, array, index + 1, size - index);
array[index] = element;
size++;
} else if (index == size) { // 相当于addLast
array[size] = element;
size++;
}*/
// 简化写法
if (index >= 0 && index < size) {
System.arraycopy(array, index, array, index + 1, size - index);
}
array[index] = element;
size++;
}
private void checkAndGrow() {
// 容量检查
if (0 == size) {
array = new int[capacity];
} else if (size == capacity) {
// 进行扩容1.5倍
capacity += capacity >> 1;
int[] newArray = new int[capacity];
System.arraycopy(array, 0, newArray, 0, size);
array = newArray;
}
}
/**
* 查询元素
* @param index 索引位置, 在 [0..size) 区间内
* @return 该索引位置的元素
*/
public int get(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
return array[index];
}
/**
* 遍历方法1
* @param consumer 遍历要执行的操作, 入参: 每个元素
*/
public void forEach1(Consumer<Integer> consumer) {
for (int i = 0; i < size; i++) {
// System.out.print(array[i] + " ");
// 提供array[i],接受的返回值为void,所以用Consumer
consumer.accept(array[i]);
}
}
/**
* 遍历方法2 - 迭代器遍历
*/
@Override
public Iterator<Integer> iterator() {
return new Iterator<Integer>() {
int i = 0;
// 有没有下一个元素
@Override
public boolean hasNext() {
return i < size;
}
// 返回当前元素,并移动到下一个元素
@Override
public Integer next() {
return array[i++];
}
};
}
/**
* 遍历方法3 - stream 遍历
* @return stream 流
*/
public IntStream forEach3() {
return IntStream.of(Arrays.copyOfRange(array, 0, size));
}
/**
* 从 [0 .. size) 范围删除元素
* @param index 索引位置
* @return 被删除元素
*/
public int remove(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
int removed = array[index];
// 删除最后一个元素时不用移动任何元素
if (index < size - 1) {
System.arraycopy(array, index + 1, array, index, size - index - 1);
}
size--;
return removed;
}
}
插入或删除性能
头部位置,时间复杂度是 $O(n)$
中间位置,时间复杂度是 $O(n)$
尾部位置,时间复杂度是 $O(1)$(均摊来说)
3、二维数组
int[][] array = {
{11, 12, 13, 14, 15},
{21, 22, 23, 24, 25},
{31, 32, 33, 34, 35},
};
内存图如下:
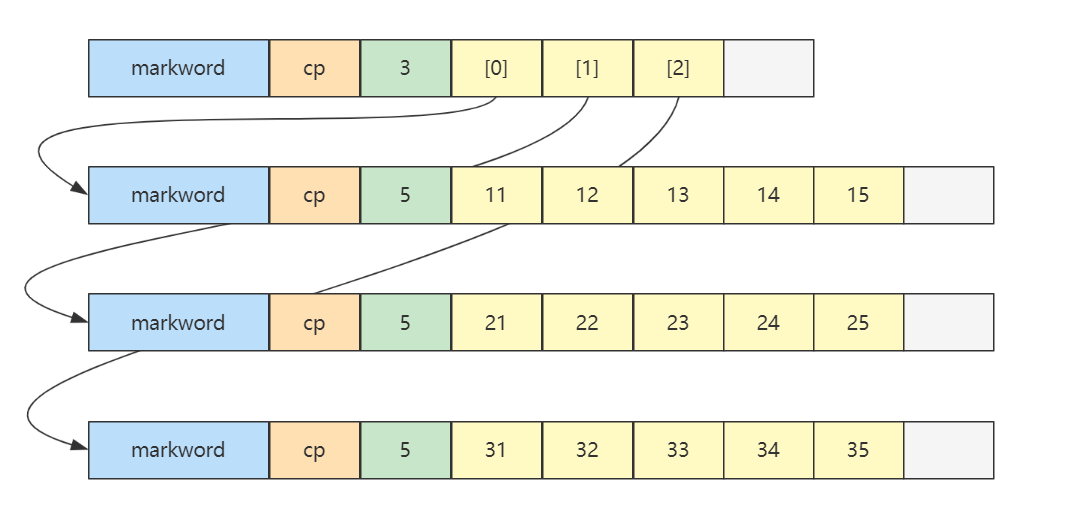
- 二维数组占 32 个字节,其中 array[0],array[1],array[2] 三个元素分别保存了指向三个一维数组的引用
-
三个一维数组各占 40 个字节
-
这四个数组在内层布局上是连续的
更一般的,对一个二维数组 $Array[m][n]$
- $m$ 是外层数组的长度,可以看作 row 行
- $n$ 是内层数组的长度,可以看作 column 列
- 当访问 $Array[i][j]$,$0\leq i \lt m, 0\leq j \lt n$时,就相当于
- 先找到第 $i$ 个内层数组(行)
- 再找到此内层数组中第 $j$ 个元素(列)
小测试
Java 环境下(不考虑类指针和引用压缩,此为默认情况),有下面的二维数组
byte[][] array = {
{11, 12, 13, 14, 15},
{21, 22, 23, 24, 25},
{31, 32, 33, 34, 35},
};
已知 array 对象起始地址是 0x1000,那么 23 这个元素的地址是什么?
分析:
- 起始地址 0x1000
- 外层数组大小:16 字节对象头 + 3 元素 * 每个引用 4 字节 + 4 对齐字节 = 32 = 0x20
- 第一个内层数组大小:16 字节对象头 + 5 元素 * 每个 byte 元素 1 字节 + 3 对齐字节 = 24 = 0x18
- 第二个内层数组,16 字节对象头 = 0x10,待查找元素索引为 2
- 最后结果 = 0x1000 + 0x20 + 0x18 + 0x10 + 2 * 1 = 0x104a
4、局部性原理
这里只讨论空间局部性
- CPU 读取内存(速度慢)数据后,会将其放入高速缓存(速度快)当中,如果后来的计算再用到此数据,在缓存中能读到的话,就不必读内存了
- 内存的读写速度是纳秒(10 的 -9 次方)级别的,而 CPU 的运算速度是皮秒(10 的 -12 次方)级别的
- 缓存的最小存储单位是缓存行(cache line),一般是 64 bytes,一次读的数据少了不划算啊,因此最少读 64 bytes 填满一个缓存行,因此读入某个数据时也会读取其临近的数据,这就是所谓空间局部性
对效率的影响
比较下面 ij 和 ji 两个方法的执行效率
public static void main(String[] args) {
int rows = 1_000_000;
int columns = 14;
int[][] a = new int[rows][columns];
StopWatch sw = new StopWatch();
sw.start("ij");
ij(a, rows, columns);
sw.stop();
sw.start("ji");
ji(a, rows, columns);
sw.stop();
System.out.println(sw.prettyPrint());
}
ij 方法:
public static void ij(int[][] a, int rows, int columns) {
long sum = 0L;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
sum += a[i][j];
}
}
System.out.println(sum);
}
ji 方法:
public static void ji(int[][] a, int rows, int columns) {
long sum = 0L;
for (int j = 0; j < columns; j++) {
for (int i = 0; i < rows; i++) {
sum += a[i][j];
}
}
System.out.println(sum);
}
执行结果:
0
0
StopWatch '': running time = 96283300 ns
---------------------------------------------
ns % Task name
---------------------------------------------
016196200 017% ij
080087100 083% ji
可以看到 ij 方法的效率比 ji 方法快很多,为什么呢?
- 缓存是有限的,当新数据来了后,一些旧的缓存行数据就会被覆盖
- 如果不能充分利用缓存的数据,就会造成效率低下
以 ji 方法执行为例,第一次内循环要读入 $[0,0]$ 这条数据,由于局部性原理,读入 $[0,0]$ 的同时也读入了 $[0,1] … [0,13]$,如图所示

但很遗憾,第二次内循环要的是 $[1,0]$ 这条数据,缓存中没有,于是再读入了下图的数据
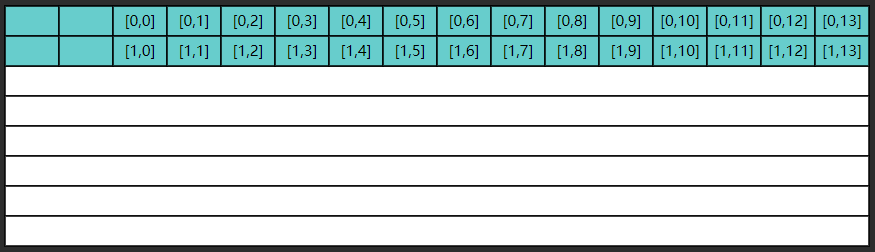
这显然是一种浪费,因为 $[0,1] … [0,13]$ 包括 $[1,1] … [1,13]$ 这些数据虽然读入了缓存,却没有及时用上,而缓存的大小是有限的,等执行到第九次内循环时
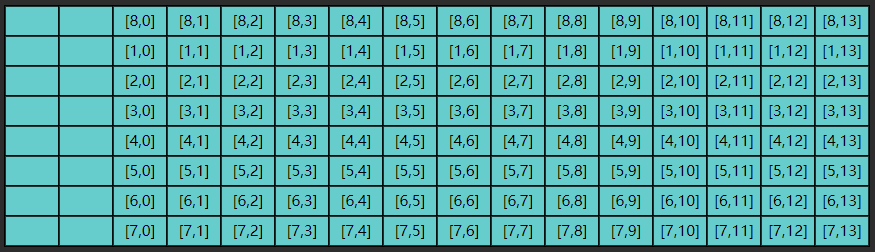
缓存的第一行数据已经被新的数据 $[8,0] … [8,13]$ 覆盖掉了,以后如果再想读,比如 $[0,1]$,又得到内存去读了
同理可以分析 ij 函数则能充分利用局部性原理加载到的缓存数据
举一反三
- I/O 读写时同样可以体现局部性原理
-
数组可以充分利用局部性原理,那么链表呢?
- 链表不行,因为链表的元素并非相邻存储
5、越界检查
Java 中对数组元素的读写都有越界检查,类似于下面的代码
bool is_within_bounds(int index) const
{
return 0 <= index && index < length();
}
代码位置:openjdk\src\hotspot\share\oops\arrayOop.hpp
只不过此检查代码,不需要由程序员自己来调用,JVM 会帮我们调用
6、习题
6.1、合并有序数组(由 Leetcode 88 改编)
将数组内两个区间内的有序元素合并
例如:
[1, 5, 6, 2, 4, 10, 11]
可以视作两个有序区间
[1, 5, 6] 和 [2, 4, 10, 11]
合并后,结果仍存储于原有空间
[1, 2, 4, 5, 6, 10, 11]
方法 1
递归
每次递归比较两个区间的第一个元素,把更小的元素复制到结果数组。过程如下面伪代码所示
merge(left=[1,5,6], right=[2,4,10,11], a2=[]) {
merge(left=[5,6], right=[2,4,10,11], a2=[1]) {
merge(left=[5,6], right=[4,10,11], a2=[1,2]) {
merge(left=[5,6], right=[10,11], a2=[1,2,4]) {
merge(left=[6], right=[10,11], a2=[1,2,4,5]) {
merge(left=[], right=[10,11], a2=[1,2,4,5,6]) {
// 拷贝10和11到a2
}
}
}
}
}
}
代码:
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2, int k) {
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
return;
}
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
return;
}
if (a1[i] < a1[j]) {
a2[k] = a1[i];
merge(a1, i + 1, iEnd, j, jEnd, a2, k + 1);
} else {
a2[k] = a1[j];
merge(a1, i, iEnd, j + 1, jEnd, a2, k + 1);
}
}
测试:
public static void main(String[] args) {
int[] a1 = {1, 5, 6, 2, 4, 10, 11};
int[] a2 = new int[a1.length];
// 测试方法一
merge(a1, 0, 2, 3, 6, a2, 0);
System.out.println(Arrays.toString(a2));
System.arraycopy(a2, 0, a1, 0, a2.length);
System.out.println(Arrays.toString(a1));
}
方法 2
思路和方法一差不多,都是比较两个区间的第一个元素,把更小的元素复制到结果数组。只不过不采用递归的形式
代码:
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
int k = 0;
while (i <= iEnd && j <= jEnd) {
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
测试:
public static void main(String[] args) {
int[] a1 = {1, 5, 6, 2, 4, 10, 11};
int[] a2 = new int[a1.length];
// 测试方法二
merge(a1, 0, 2, 3, 6, a2);
System.out.println(Arrays.toString(a2));
}