一、题目
给你二叉树的根节点 root ,返回它节点值的 前序 遍历
示例 1:
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/binary-tree-preorder-traversal
二、题解
二叉树的递归遍历很简单,递归通常是用栈来实现的,那如何用栈来实现二叉树的非递归遍历呢?
基础迭代
前序遍历是中左右,每次先处理的是中间节点,那么先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。为什么要先加入右孩子,再加入左孩子呢? 因为这样出栈的时候才是中左右的顺序,栈的特点就是先进后出。

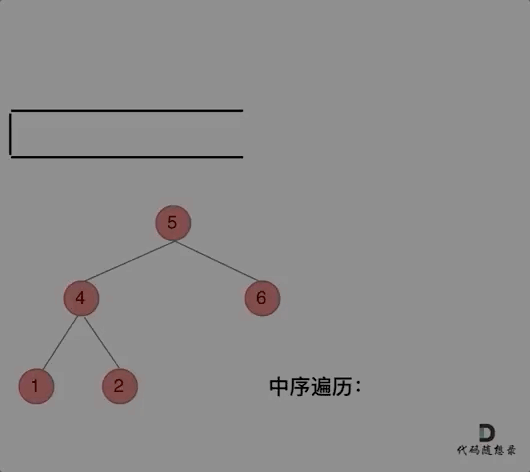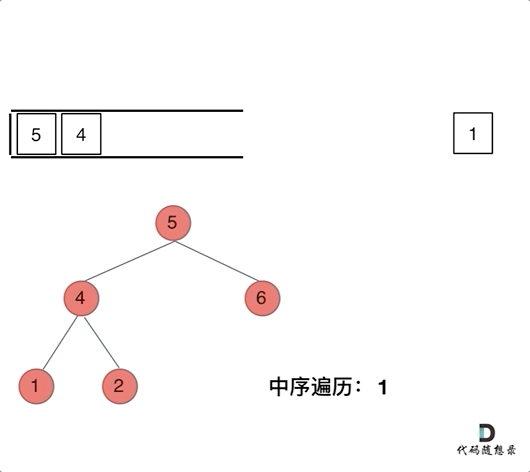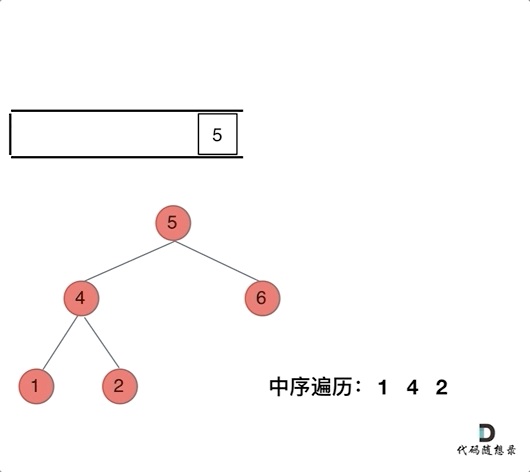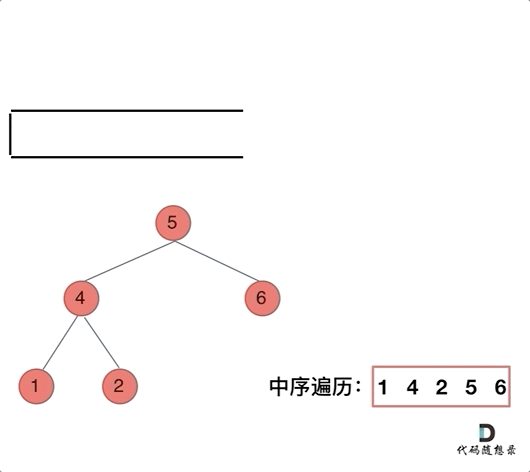
而对于中序遍历,无法直接应用前序遍历的逻辑,因为前序遍历要访问的元素和要处理的元素顺序是一致的,都是中间节点。但中序遍历是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进 result 数组中),这就造成了处理顺序和访问顺序是不一致的。那么在使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
再来看后序遍历。先序遍历是中左右,后序遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后再反转 result 数组,输出的结果顺序就是左右中了。所以后序遍历只需要前序遍历的代码稍作修改就可以了。(这想法有点奇妙,换成自己真不一定想得出来)
统一迭代
对于三种遍历方式,如何使用迭代法写出统一风格的代码,实现了其中的一种遍历方式,其他两种只要稍稍改一下节点顺序就可以了呢?
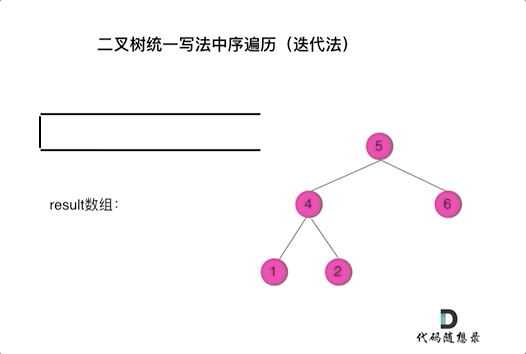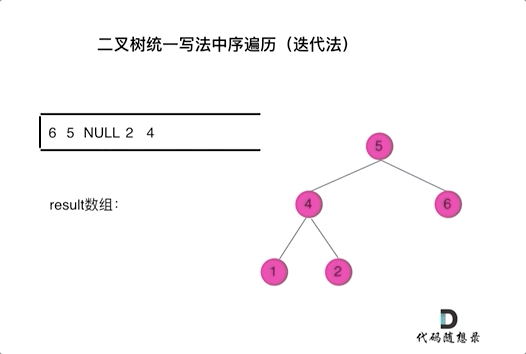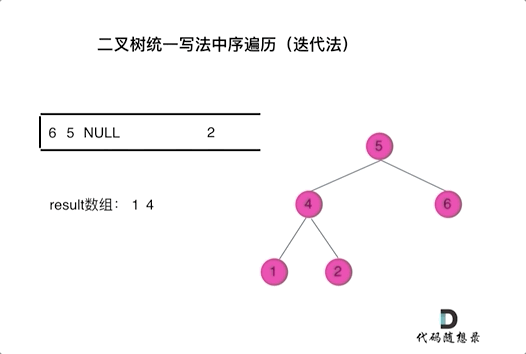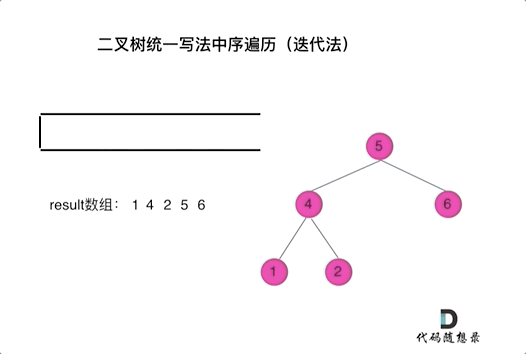
以中序遍历为例,使用栈的话,无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。那就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
如何标记呢?
- 方法一:要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法可以叫做空指针标记法。这样只有空节点弹出的时候,才将下一个节点放进结果集。(自己手动模拟一遍整个过程才体会到这方法也太妙了吧,不知道谁想出来的)。
- 方法二:加一个
boolean值跟随每个节点,false(默认值)表示需要为该节点和它的左右儿子安排在栈中的位次,true表示该节点的位次之前已经安排过了,可以收割节点了。这种方法可以叫做 boolean 标记法,这种方法更容易理解,在面试中更容易写出来。
用统一迭代法写前序遍历和后序遍历时,只需要在中序遍历基础上仅仅改变了添加左右子树的两行代码的顺序即可,这就是统一迭代法的厉害之处!
三、代码
基础迭代
class Traverse {
// 前序遍历非递归遍历
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if (root == null) {
return result;
}
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
// 注意空节点不入栈
if (node.right != null)
stack.push(node.right);
if (node.left != null)
stack.push(node.left);
}
return result;
}
// 中序遍历非递归遍历
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
// 当指针和栈都为空时,才说明遍历和处理节点都已完成
// 所以while循环的条件是or而不是and
while (cur != null || !stack.isEmpty()) {
// 指针先一路向左遍历,将遍历到的节点入栈。直到最下面最左边的节点入栈后,
// 指针为空,此时开始弹出栈顶元素,将其添加到result数组。
// 然后指针开始往回走,向右遍历
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop();
result.add(cur.val);
cur = cur.right;
}
}
return result;
}
// 后序遍历非递归遍历
public List<Integer> postorderTraversal2(TreeNode root) {
List<Integer> result = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if (root == null) {
return result;
}
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null)
stack.push(node.left);
if (node.right != null)
stack.push(node.right);
}
Collections.reverse(result);
return result;
}
}
统一迭代
前序遍历:
// 前序遍历统一迭代法之空指针标记法
public List<Integer> preorderTraversal3(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
// 如果此处用pop而不是peek,则if和else里的pop语句都应该去掉,防止多弹出元素
// TreeNode node = stack.pop();
TreeNode node = stack.peek();
if (node != null) {
stack.pop();
if (node.right != null)
stack.push(node.right);
if (node.left != null)
stack.push(node.left);
stack.push(node);
stack.push(null);
} else {
stack.pop();
node = stack.pop();
result.add(node.val);
}
}
return result;
}
// 前序遍历统一迭代法之boolean标记法
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Stack<AbstractMap.SimpleEntry<TreeNode, Boolean>> stack = new Stack<>();
stack.push(new AbstractMap.SimpleEntry<>(root, false));
while (!stack.isEmpty()) {
TreeNode node = stack.peek().getKey();
// 多加一个visited参数,使“迭代统一写法”成为一件简单的事
boolean visited = stack.peek().getValue();
stack.pop();
// visited为True,表示该节点和两个儿子位次之前已经安排过了,现在可以收割节点了
if (visited) {
result.add(node.val);
continue;
}
// visited当前为false, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”
// 前序遍历是'中左右',右儿子最先入栈,最后出栈
if (node.right != null) {
stack.push(new AbstractMap.SimpleEntry<>(node.right, false));
}
// 左儿子位置居中
if (node.left != null) {
stack.push(new AbstractMap.SimpleEntry<>(node.left, false));
}
// 节点自己最后入栈,最先出栈
// 同时设置visited为true,表示下次再访问本节点时,允许收割
stack.push(new AbstractMap.SimpleEntry<>(node, true));
}
return result;
}
后序遍历:
// 后序遍历统一迭代法之空指针标记法
public List<Integer> postorderTraversal3(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
// 如果此处用pop而不是peek,则if和else里的pop语句都应该去掉,防止多弹出元素
// TreeNode node = stack.pop();
TreeNode node = stack.peek();
if (node != null) {
stack.pop();
stack.push(node);
stack.push(null);
if (node.right != null)
stack.push(node.right);
if (node.left != null)
stack.push(node.left);
} else {
stack.pop();
node = stack.pop();
result.add(node.val);
}
}
return result;
}
// 后序遍历统一迭代法之boolean标记法
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Stack<AbstractMap.SimpleEntry<TreeNode, Boolean>> stack = new Stack<>();
stack.push(new AbstractMap.SimpleEntry<>(root, false));
while (!stack.isEmpty()) {
TreeNode node = stack.peek().getKey();
// 多加一个visited参数,使“迭代统一写法”成为一件简单的事
boolean visited = stack.peek().getValue();
stack.pop();
// visited为True,表示该节点和两个儿子位次之前已经安排过了,现在可以收割节点了
if (visited) {
result.add(node.val);
continue;
}
// visited当前为false, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”
// 后序遍历是'左右中',节点自己最先入栈,最后出栈
// 同时设置visited为true,表示下次再访问本节点时,允许收割
stack.push(new AbstractMap.SimpleEntry<>(node, true));
// 右儿子位置居中
if (node.right != null) {
stack.push(new AbstractMap.SimpleEntry<>(node.right, false));
}
// 左儿子最后入栈,最先出栈
if (node.left != null) {
stack.push(new AbstractMap.SimpleEntry<>(node.left, false));
}
}
return result;
}
中序遍历:
// 中序遍历统一迭代法之空指针标记法
public List<Integer> inorderTraversal3(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
// 如果此处用pop而不是peek,则if和else里的pop语句都应该去掉,防止多弹出元素
// TreeNode node = stack.pop();
TreeNode node = stack.peek();
if (node != null) {
stack.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node.right != null)
stack.push(node.right);// 添加右节点(空节点不入栈)
stack.push(node); // 添加中节点
stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记
if (node.left != null)
stack.push(node.left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
stack.pop(); // 将空节点弹出
node = stack.pop(); // 重新取出栈中元素
result.add(node.val); // 加入到结果集
}
}
/*
手动模拟一下整个过程便会发现,对于每棵树包括子树,都是根节点先入栈再出栈,
然后按右子树根节点左子树的顺序入栈。因为中序遍历是左中右,入栈得反着来
另外,左子树和根节点都是开始入栈时就添加了空节点,而右子树都是部分元素出栈后,
它们才又出栈一次,再入栈并添加空节点。总之,每个节点后面都会有一个空节点
*/
return result;
}
// 中序遍历统一迭代法之boolean标记法
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Stack<AbstractMap.SimpleEntry<TreeNode, Boolean>> stack = new Stack<>();
stack.push(new AbstractMap.SimpleEntry<>(root, false));
while (!stack.isEmpty()) {
TreeNode node = stack.peek().getKey();
// 多加一个visited参数,使“迭代统一写法”成为一件简单的事
boolean visited = stack.peek().getValue();
stack.pop();
// visited为True,表示该节点和两个儿子位次之前已经安排过了,现在可以收割节点了
if (visited) {
result.add(node.val);
continue;
}
// visited当前为false, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”
// 中序遍历是'左中右',右儿子最先入栈,最后出栈
if (node.right != null) {
stack.push(new AbstractMap.SimpleEntry<>(node.right, false));
}
// 把自己加回到栈中,位置居中
// 同时设置visited为true,表示下次再访问本节点时,允许收割
stack.push(new AbstractMap.SimpleEntry<>(node, true));
// 左儿子最后入栈,最先出栈
if (node.left != null) {
stack.push(new AbstractMap.SimpleEntry<>(node.left, false));
}
}
return result;
}